Deep Learning for Spatial and Spatio-Temporal Statistics

This page outlines work done at the Centre for Environmental Informatics within NIASRA at the University of Wollongong, Australia, since 2018, on the application of deep learning models to spatial and spatio-temporal statistical models. This work was in large part funded by the Australian Research Council (ARC) Discovery Early Career Research Award (DECRA) DE180100203 awarded to Andrew Zammit-Mangion.

About Me

My name is Andrew Zammit-Mangion and I am an Associate Professor in Statistics with the National Institute for Applied Statistics Research Australia (NIASRA) at the University of Wollongong. I completed my PhD in 2012 at the University of Sheffield, UK in the Department of Automatic Control and Systems Engineering before carrying out brief post-docs at the University of Edinburgh with the School of Informatics and the University of Bristol with the Department of Maths and the School of Geographical Sciences. I joined NIASRA in 2014.

This page highlights some of the key projects I have participated in with some great students and collaborators as part of the Discovery Early Career Research Award (DECRA) that I was awarded in 2017, titled ‘Deep space-time models for modelling complex environmental phenomena’ (see Collaborators and Students). The DECRA was invaluable in giving me the time to explore some ideas that I had for several years since my time in the UK, and to connect with several international researchers. Please take a browse through the below key projects; the synopsis for each project is deliberately short, and clicking on ‘Read more’ will direct you to a published work with more details.

If you would like to follow me on Twitter, my handle is @andrewzm.

Key Projects

Deep Compositional Spatial Models

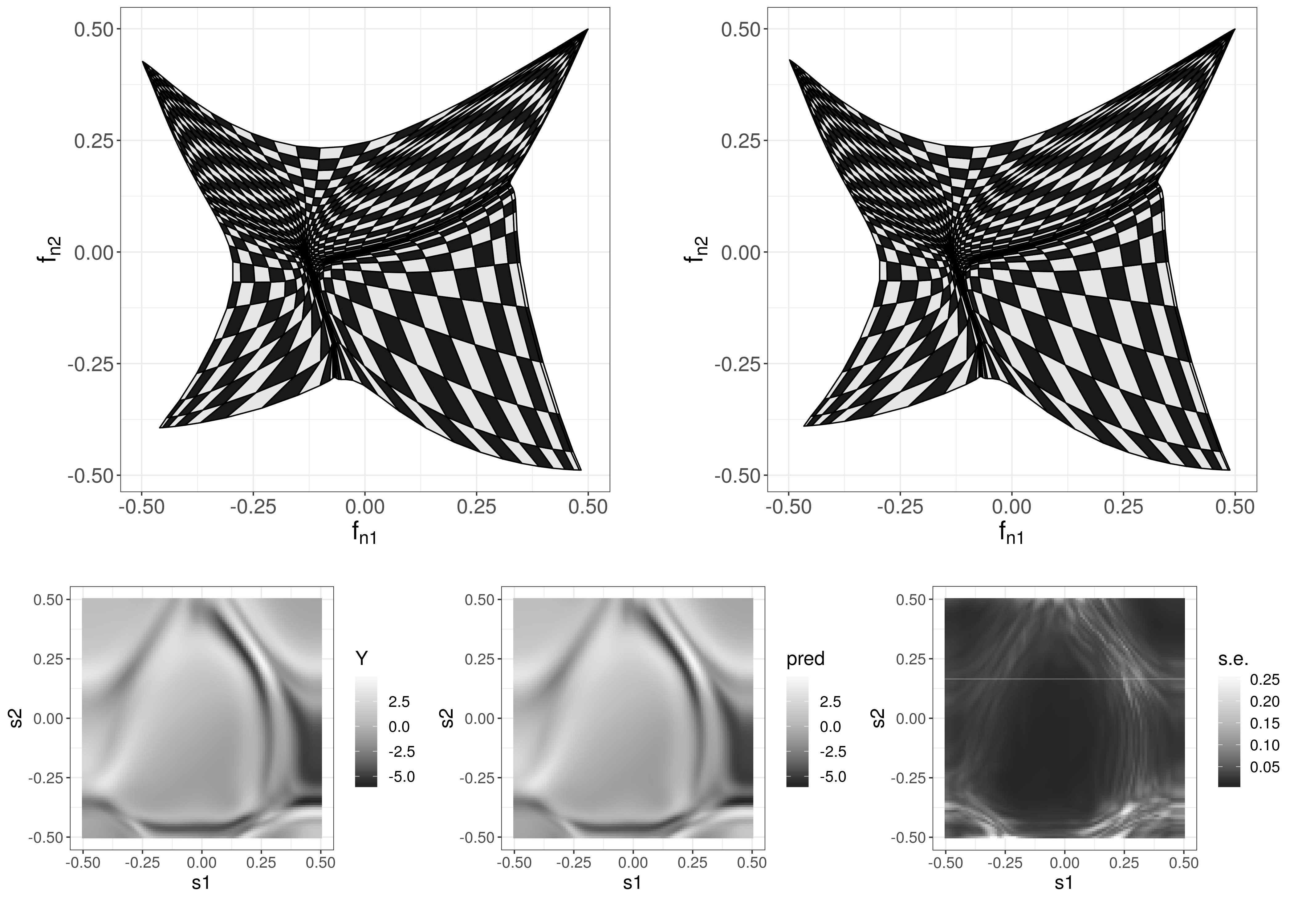
Nonstationarity in spatial processes can be constructed by warping space and subsequently defining a stationary process on the warped domain. In this project, together with James Ng, Quan Vu, and Maurizio Filippone, we describe a warping approach that allows for straightforward fitting and prediction with univariate spatial data. The model is constructed from low-dimensional injective warping functions which can either be estimated using maximum likelihood or inferred using stochastic variational Bayes.

Multivariate Deep Compositional Spatial Models

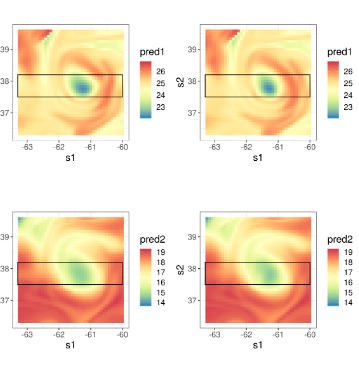
In this project led by Quan Vu, and together with Noel Cressie, we extend the deep compositional spatial models outlined in the previous project to the multivariate case. Here, we model the joint processes using stationary, symmetric, covariance functions on the warped domain. There are many interesting properties that emerge when modelling nonstationarity and asymmetry of multivariate spatial processes in this way.

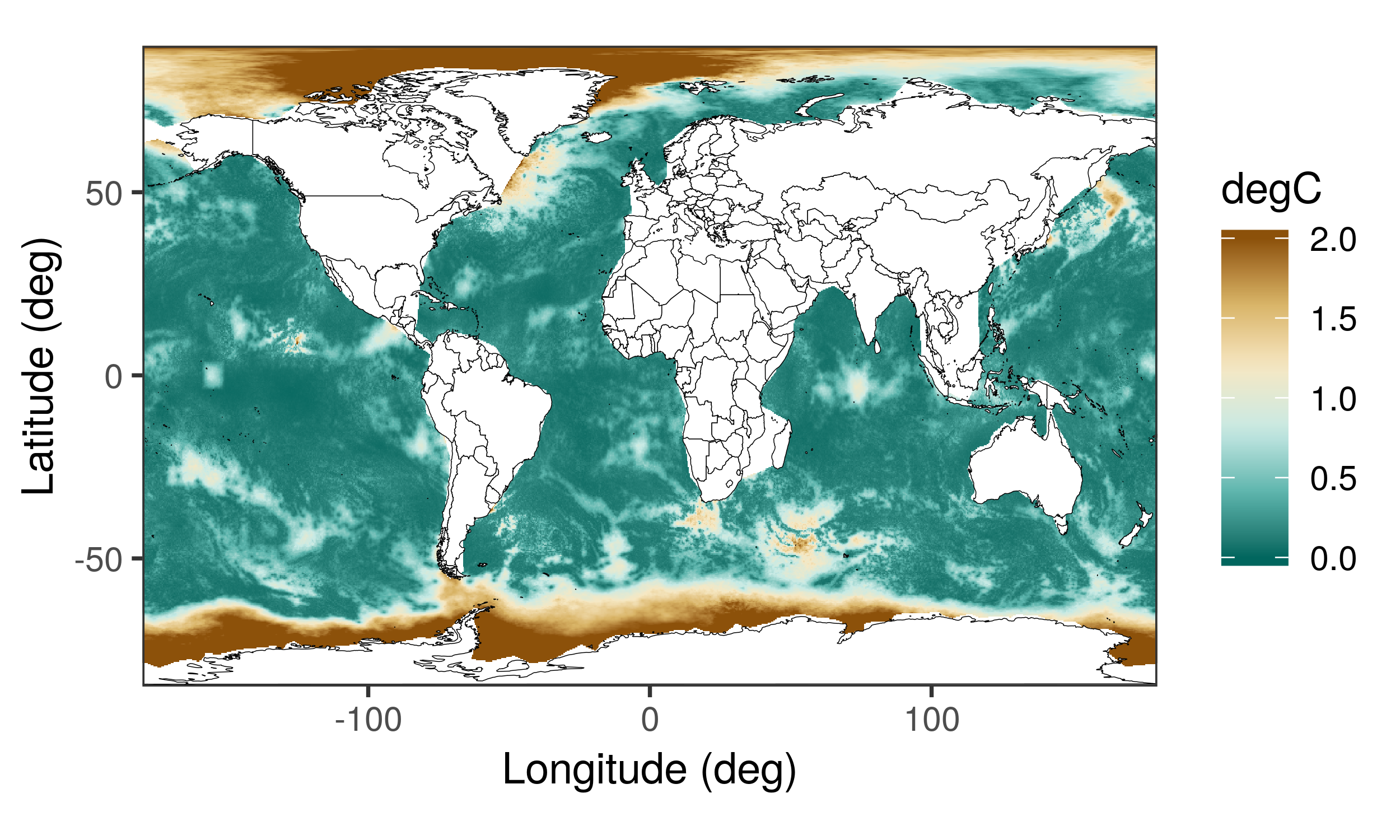
Convolutional Neural Network Spatio-Temporal Models

Dynamic spatio-temporal models are often used to model highly dynamic geophysical or ecological processes, such as daily sea-surface temperature or the spread of an invading species. Often, the dynamics themselves (e.g., the direction of flow) changes rapidly in both space and time. In this project, together with Chris Wikle, we integrate a convolutional neural network with a statistical spatio-temporal model to jointly predict the spatio-temporal varying dynamical parameters and the process of interest.

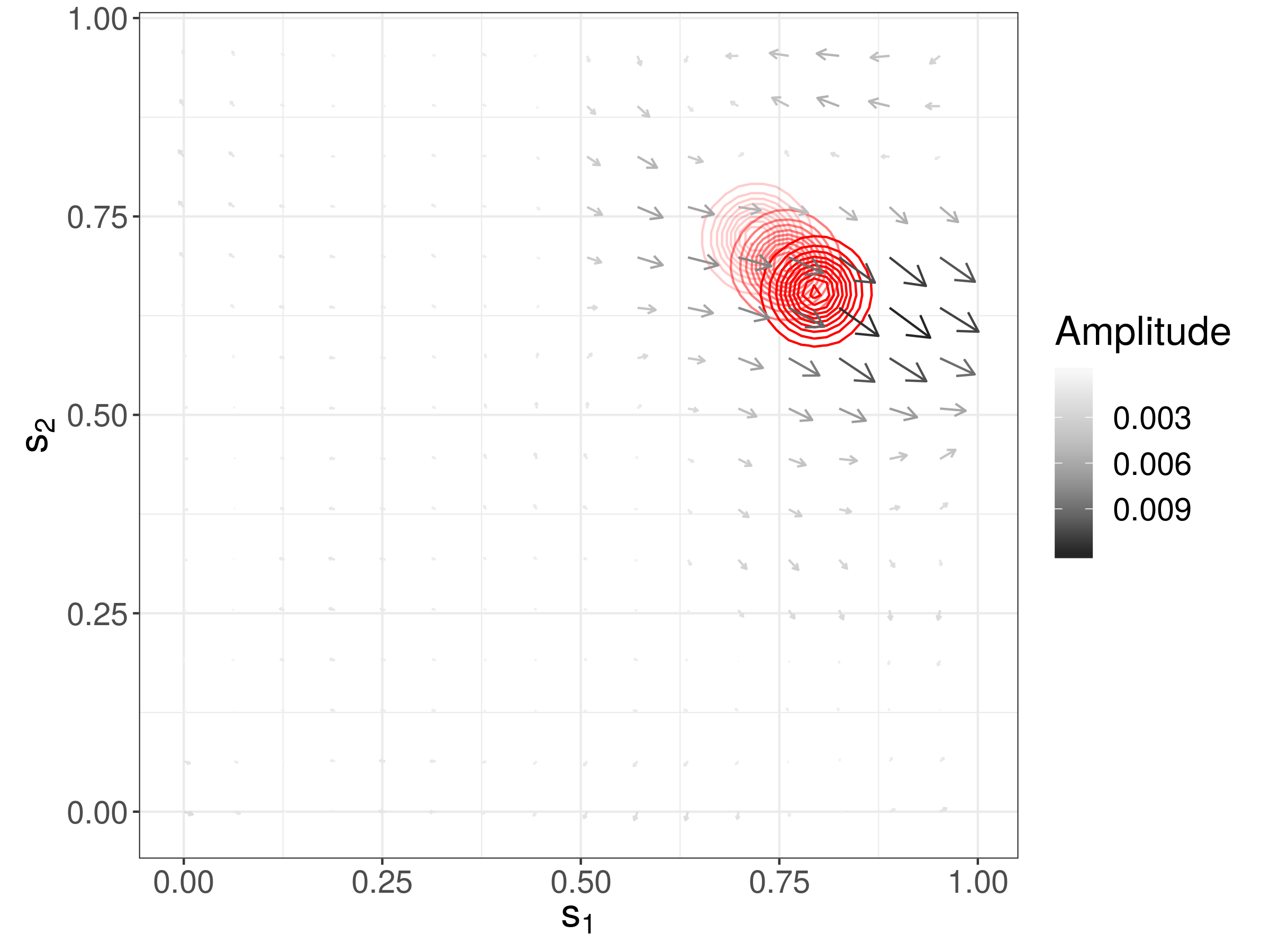
Intensity Function Estimation on the Plane using Neural Autoregressive Flows

Neural autoregressive flows are injective maps constructed using deep neural networks, often used for density estimation or for variational inference in machine learning. In this project led by James Ng, we use normalising flows to estimate the intensity function of a non-homogeneous Poisson process on the plane. We also show that the modelling architecture we use exhibits an attractive universal approximation property.

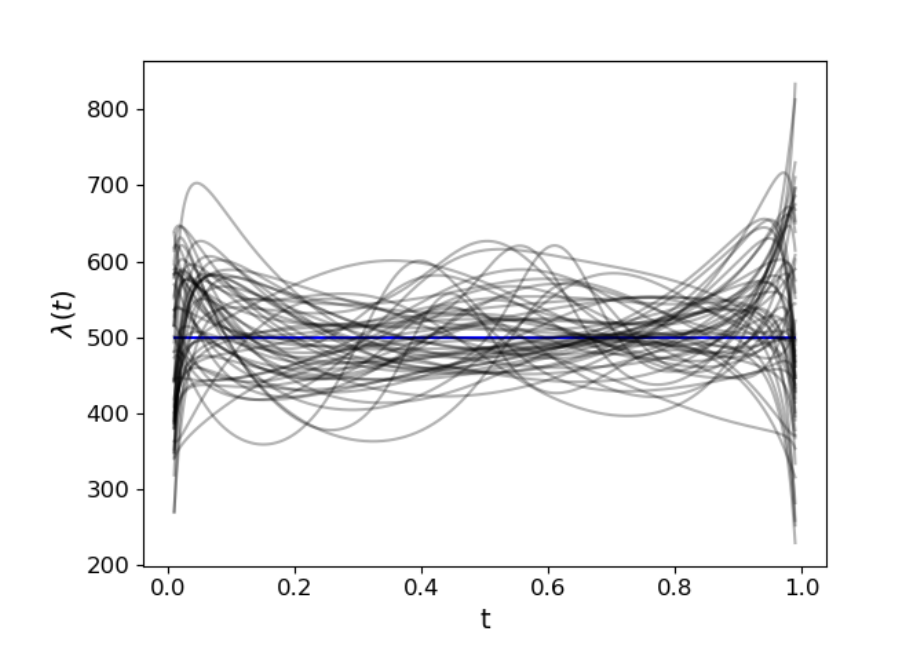
Intensity Function Estimation on the Sphere using Radial Flows

Geophysical event data (e.g., earthquake occurrence) are often presented to the analyst as a set of spherical coordinates. Here, in this project led by James Ng, we use radial flows within a measure transport framework to constuct a flexible model for the intensity function of a non-homogeneous point process on the sphere.

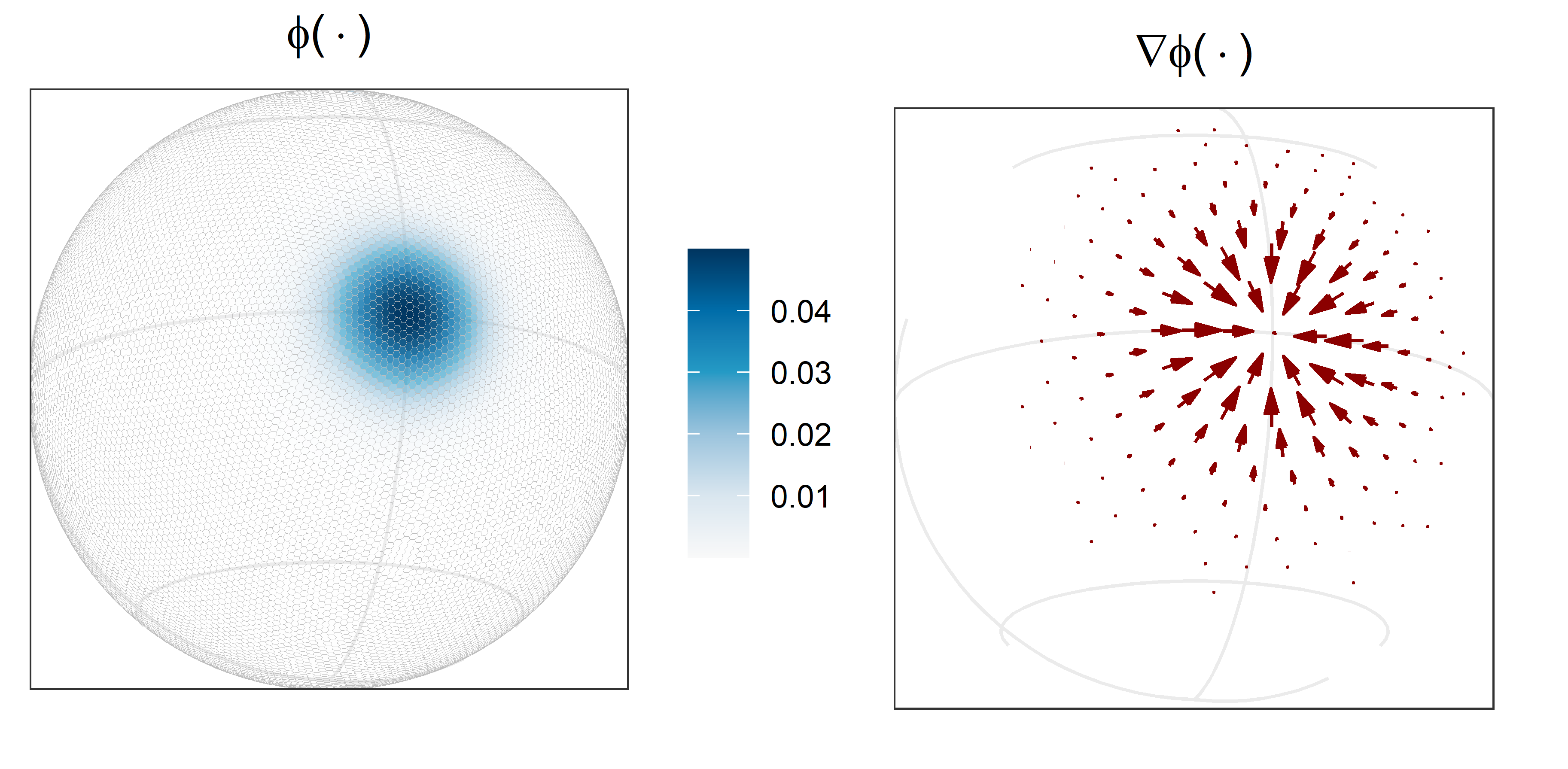
Likelihood-Free Parameter Estimation with Neural Bayes Estimators

Estimating parameters in a statistical model is often the computational bottleneck of a data analysis. Here, in a project with Matthew Sainsbury-Dale and Raphaël Huser, we use neural networks to facilitate estimation; specifically, we train neural networks to approximate Bayes estimators. These estimators are lightning fast, likelihood-free, and can yield bootstrap intervals essentiall `for free’.

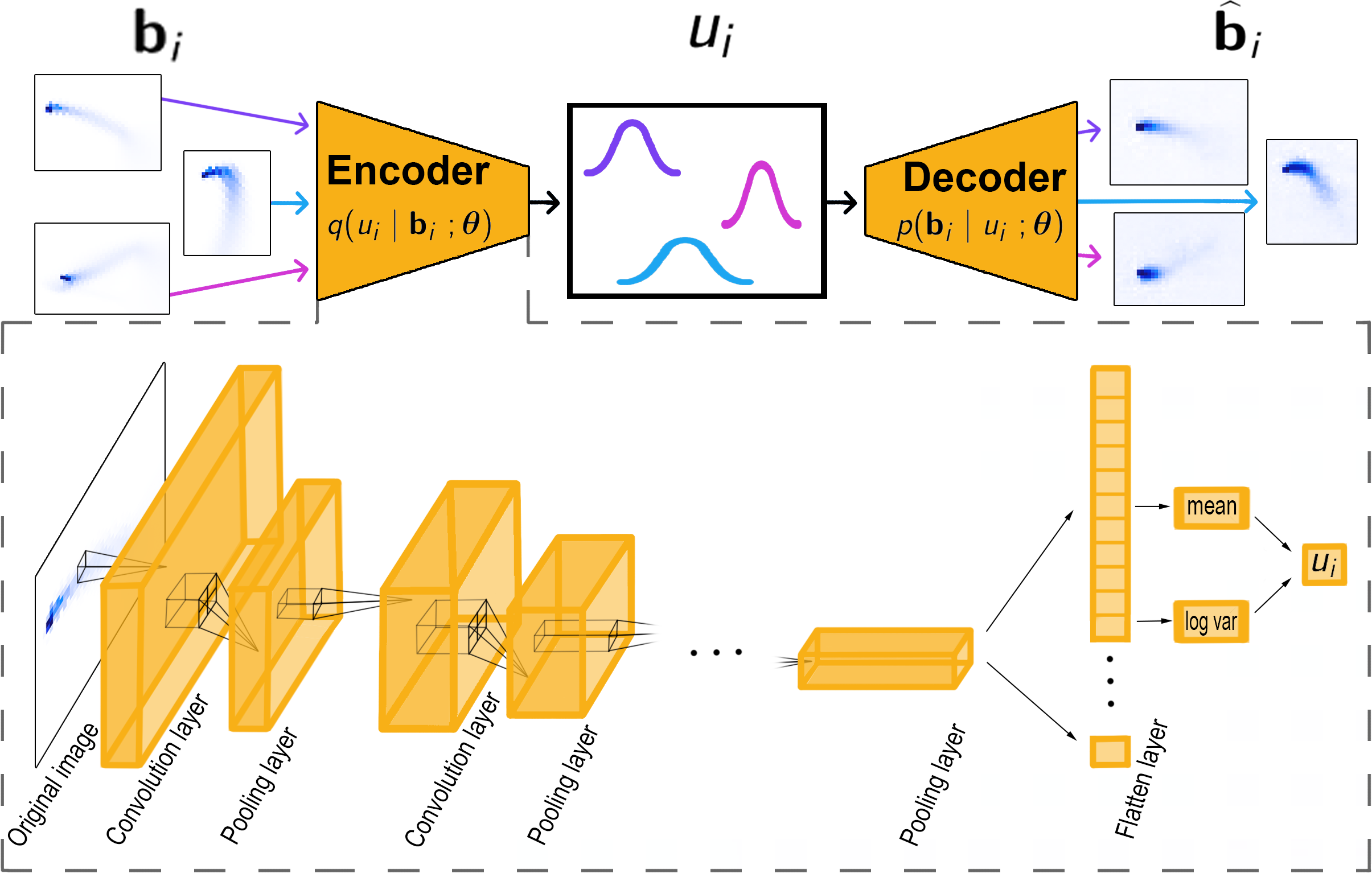
Spatio-Temporal Emulation using Convolutional Variational Autoencoders

Some computationally-intensive numerical models, such as Lagrangian Particle Dispersion Models (LPDMs), take a spatio-temporal location as an input (e.g., a source location) and generate a spatio-temporal output (e.g., the spatio-temporal evolution of a gas). In this project, led by Laura Cartwright, and together with Nicholas Deutscher, we take advantage of spatial and temporal correlations of the numerical-model output to emulate outputs at other, new, input locations. Emulation is done on a small-dimensional space constructed via a convolutional variational autoencoder.

Multi-Resolution Spatial Modelling

Fitting spatial models to big remote sensing data is often challenging even if the model one is fitting is relatively simple. However, in order to take advantage of the information in big data sets, one also needs to use more complex models. Here, together with Jonathan Rougier, we construct a spatial model that takes into account multiple spatial scales, and where the degree of spatial nonstationarity is allowed to increase with decreasing process scale.