The package FRK is available on CRAN! To install, please type
install.packages("FRK")To install the most recent development version, please load devtools and type
install_github("andrewzm/FRK", dependencies = TRUE, build_vignettes = TRUE)A paper introducing the package is available here. A paper detailing the approach in a non-Gaussian setting is available here (a six-page summary of this paper is available here).
The vignette “FRK_intro” summarises the package, gives details on the EM algorithm that may be employed in a Gaussian setting, and provides several examples. Another vignette, “FRK_non-Gaussian”, summarises inference in a non-Gaussian setting (where a Laplace approximation is used), and contains examples using non-Gaussian data and the newly available plotting methods. To access the vignettes, please click on the following links:
Tutorial on modelling spatial and spatio-temporal non-Gaussian data with FRK
A pkgdown page is also available here.
Supporting and citing
If you use FRK in your work, research, or other activities, please cite it using the information provided by citation("FRK").
Description
Package: FRK
Type: Package
Title: Fixed Rank Kriging
Version: 2.3.1
Date: 2024-07-16
Author: Andrew Zammit-Mangion, Matthew Sainsbury-Dale
Maintainer: Andrew Zammit-Mangion andrewzm@gmail.com
Description: A tool for spatial/spatio-temporal modelling and prediction with large datasets. The approach models the field, and hence the covariance function, using a set of basis functions. This fixed-rank basis-function representation facilitates the modelling of big data, and the method naturally allows for non-stationary, anisotropic covariance functions. Discretisation of the spatial domain into so-called basic areal units (BAUs) facilitates the use of observations with varying support (i.e., both point-referenced and areal supports, potentially simultaneously), and prediction over arbitrary user-specified regions. FRK also supports inference over various manifolds, including the 2D plane and 3D sphere, and it provides helper functions to model, fit, predict, and plot with relative ease. Version 2.0.0 and above also supports the modelling of non-Gaussian data (e.g., Poisson, binomial, negative-binomial, gamma, and inverse-Gaussian) by employing a generalised linear mixed model (GLMM) framework. Zammit-Mangion and Cressie (2021) describe FRK in a Gaussian setting, and detail its use of basis functions and BAUs, while Sainsbury-Dale et al. (2024) describe FRK in a non-Gaussian setting; two vignettes are available that summarise these papers and provide additional examples.
- Zammit-Mangion, A. & Cressie N. (2021). “FRK: an R package for spatial and spatio-temporal prediction with large datasets.” Journal of Statistical Software, 98, 1-48. doi:10.18637/jss.v098.i04.
- Sainsbury-Dale, M., Zammit-Mangion, A. & Cressie, N. (2024). “Modelling big, heterogeneous, non-Gaussian spatial and spatio-temporal data using FRK.” Journal of Statistical Software, 108(10), 1-39. doi:10.18637/jss.v108.i10.
License: GPL (>= 2)
Quick start
Gaussian data
library("FRK")
library("sp")
library("ggplot2")
library("ggpubr")
## Setup
m <- 1000 # Sample size
RNGversion("3.6.0"); set.seed(1) # Fix seed
zdf <- data.frame(x = runif(m), y= runif(m)) # Generate random locs
zdf$z <- sin(8 * zdf$x) + cos(8 * zdf$y) + 0.5 * rnorm(m) # Simulate data
coordinates(zdf) = ~x+y # Turn into sp object
## Run FRK
S <- FRK(f = z ~ 1, # Formula to FRK
list(zdf), # All datasets are supplied in list
n_EM = 10) # Max number of EM iterations
pred <- predict(S) # Prediction stage
## Plotting
plotlist <- plot(S, pred)
ggarrange(plotlist = plotlist, nrow = 1, legend = "top")
Non-Gaussian data
Here we analyse simulated Poisson data. We signify a Poisson data model with a mean response that is modelled using the square-root link function by setting response = "poisson" and link = "sqrt" in FRK(). Other non-Gaussian response distributions available in FRK are the binomial, negative-binomial, gamma, and inverse-Gaussian distributions.
## Simulate Poisson data using the previous example's data to construct a mean
zdf$z <- rpois(m, lambda = zdf$z^2)
## Run FRK
S <- FRK(f = z ~ 1, list(zdf),
response = "poisson", # Poisson data model
link = "sqrt") # square-root link function
pred <- predict(S)
## Plotting
plotlist <- plot(S, pred$newdata)
ggarrange(plotlist$z, plotlist$p_mu, plotlist$interval90_mu,
nrow = 1, legend = "top")
Spatio-temporal data
We now analyse spatio-temporal data, using the NOAA dataset.
## Setup
library("spacetime")
data("NOAA_df_1990")
Tmax <- subset(NOAA_df_1990, month %in% 7 & year == 1993)
Tmax <- within(Tmax, {time = as.Date(paste(year,month,day,sep="-"))})
STObj <- stConstruct(x = Tmax, space = c("lon","lat"), time = "time", interval = TRUE)
## BAUs: spatial BAUs are 1x1 pixels, temporal BAUs are 1 day intervals
BAUs <- auto_BAUs(manifold = STplane(),
cellsize = c(1, 1, 1),
data=STObj, tunit = "days")
BAUs$fs <- 1 # scalar fine-scale variance matrix, implicit in previous examples
## Basis functions
G <- auto_basis(manifold = STplane(), data = STObj, nres = 2, tunit = "days")
## Run FRK
STObj$std <- 2 # fix the measurement error variance
S <- FRK(f = z ~ 1 + lat, data = list(STObj),
basis = G, BAUs = BAUs, est_error = FALSE, method = "TMB")
pred <- predict(S, percentiles = NULL)
## Plotting: include only some times via the argument subset_time
plotlist <- plot(S, pred$newdata, subset_time = c(1, 7, 13, 19, 25, 31))
ggarrange(plotlist = plotlist, nrow = 1, legend = "top")
Demonstrations
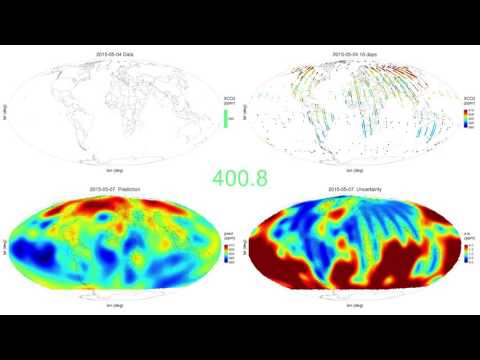
The package FRK is currently being used to generate spatio-temporal animations of fields observed by satellite data. Here we show a daily prediction of CO2 using data from the NASA OCO-2 between September 2014 and June 2016.
Acknowledgements
Thanks to Michael Bertolacci for designing the FRK hex logo!